混合有限元网格

题目

Mixed Finite Elements for Variational Surface Modeling

概述

这篇文章可能比较偏学术一点，作者提出了一个常见的偏微分方程的离散采用混合有限元网格的方法，引入更多变量的导数。

这种方法使用一阶导数，允许一个简单的线性元件离散。在这个设定下，各种边界条件可以是自然离散的。格式化连续区域的限制，并显示这些无缝贴合的混合框架。证明在有限元模型中混合FEM，不同的建模任务，并分析它的有效性和收敛性。

论文内容

论文背景

探讨各种类型混合离散网格的收敛特性和假设的离散网格的依赖程度，展示了几个应用程序的混合框架的几何造型，如互动的形状编辑，孔填充，共混物，和表面的修补程序的边界曲线。

模型问题

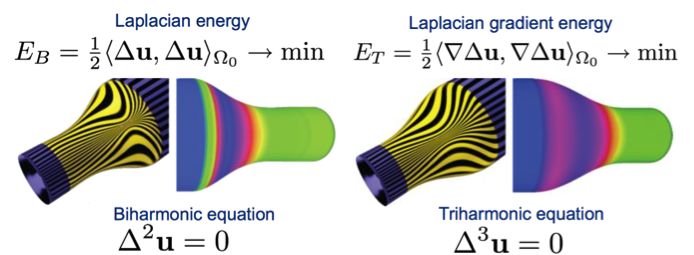
我们考虑两个重要的例子：拉普拉斯算子和拉普拉斯梯度能量，引入双调和（biharmonic）和三调和（triharmonic）方程

在第一个问题中我们计算变形U平面Ω0使拉普拉斯能量最小化

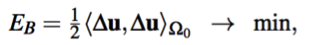
第二个例子是带有边界条件的二阶导数的拉普拉斯梯度能量，曲率连续曲面建模的重要性。

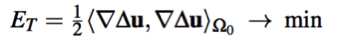
所以最小化之后的效果示意如下图

低阶分解：

一般的系统的方法来解决问题，涉及高阶导数的离散化是一个无约束的优化问题

边界条件类型：

在连续的情况下，我们定义了各种边界条件。虽然对于某些应用程序（例如，变形的固定网格）的问题，可以完全在离散域的研究，当一个共同的参考点是必要的网格具有不同的连接和分辨率，接近相同的形状。

边界条件可以用不同尺寸的域Ω0亚群相关：

• 区域边界条件的开放领域ΩF⊂Ω0；如下图：

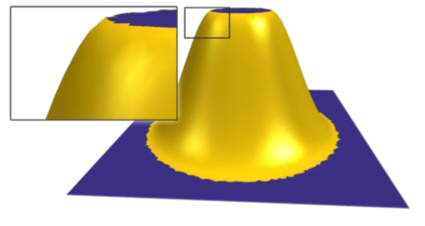
• 曲线边界条件对曲线C⊂Ω0

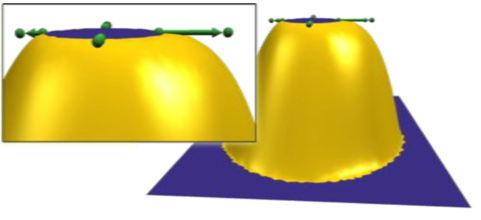
• 点边界条件对孤立点P∈Ω0

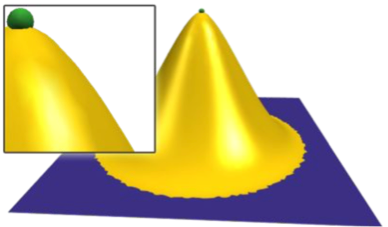
混合有限元离散化

拉普拉斯能量和双调和方程

一个取代了首项的帕普拉斯方程如下：

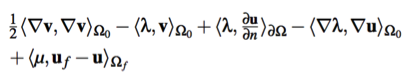
1. 分段线性单元的离散化：

   a) 仅用一阶导数表示

   b) 使用平均值作为顶点区域的能量，通常用于几何建模

   c) 没有明显的连接到连续的情况

2. 混合元素

   a) 引入附加变量将高阶问题转换为低阶

   b) 离散变量使用分段线性逼近

   c) 集总矩阵（Lumped mass matrices）

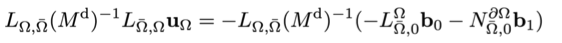
1. 固定曲线条件

   a) 利用拉格朗日强制执行区域条件

   b) 离散变量使用分段线性逼近

   c) 消除aux.变量

2. 收敛

拉普拉斯能量和三调和方程

1. 曲线边界条件

   a) 固定部分网格外求解区域

   b) 曲线to区域

   c) 固定边界曲线

   d) 环状进入内部指定曲率

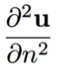
2. 减少固定曲线边界条件

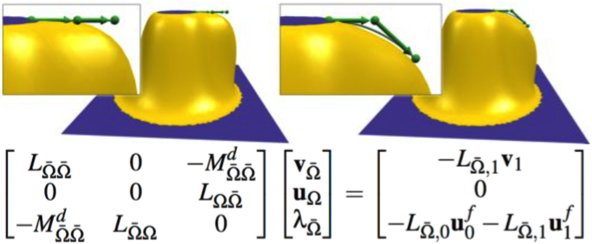
1. 收敛

实现

测试系统的收敛，随机产生的不规则域。一个顶点放置在每个网格中的每个方格中，参数控制的变化规律，用三角形库连接，控制最小的内角

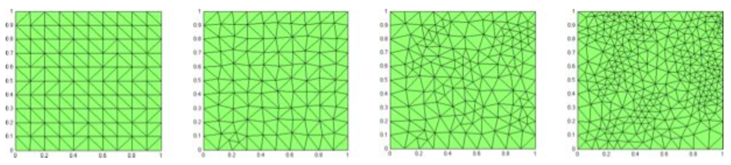
填孔：拉普拉斯能量

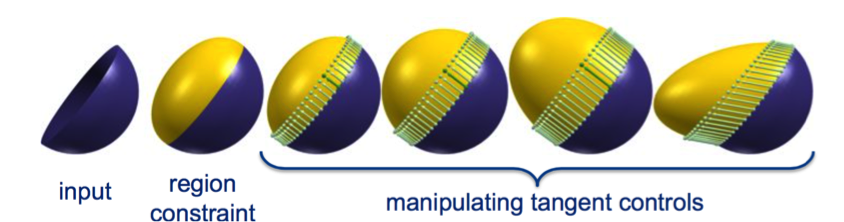
能量或偏微分方程的离散化技术：

• 通过引入变量降到低阶

• 用约束来强制执行区域边界条件

• 块质量矩阵

收敛第四和第六阶偏微分方程

心得

一开始是看到这篇文章的几个相关视频，觉得十分有趣，才去看了这篇文章，不过没想到学术性十分强烈。确实又碰到比较难看懂的一篇。不过幸好里面所用到的拉普拉斯算子之类的在课堂上就有接触过，所以还不至于很陌生，硬啃下来还是看懂了大概的过程。

不过这篇论文好像也还是比较浅层面的运算，另外有一篇比较深入地推导过程的我就没有看。

这篇论文其实有对应的应用的，是在三维层面上对模型进行的一些拉伸操作还有变形，也是建立在拉普拉斯上面的，不过在论文里面没有体现，所以我周报里面也没有涉及。